除以零

如果出现文字缺失，格式混乱请取消转码/退出阅读模式

這麼說來，你發現不了錯誤？

他搖搖頭。發現不了。我滑進了和你相同的套路:只能用你的方法思考這個問題。

雷內卻已經不在老套路上了:她另闢蹊徑，想出了一條截然不同的路子來解決這個問題，但卻僅僅證明了原先的體系確實存在矛盾。不過，還是謝謝你費心了。

你要另外找人看一看嗎？

是的。我想我要寄給伯克利的卡拉漢看。自去年天那次會議以來，我們一直保持著聯繫。

法布里希點了點頭，他上次發表的一篇文章真的給我留下很深的印象。如果他發現了問題，請一定告訴我。我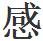到很好奇。

雷內寧願用比好奇更強烈的字眼來表達她自己的心情。

5b雷內對自己的研究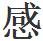到絕望了嗎？卡爾知道她從來不覺得數學真的困難，而只是一種智力挑戰。難道是她第一次遇到無法突破的難題嗎？或者說，數學本身就是無解的嗎？嚴格說來，卡爾自己是一個實驗主義者，並不真正懂得雷內怎麼創造新的數學體系。雖說聽上去有點傻，但是她是靈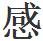枯竭了嗎？

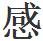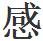雷內是成年人，不會像神童那樣，發現自己正在成為平庸的成年人而到幻滅的痛苦。另一方面，許多數學家在三十歲之前就達到事業的巔峰。雖然她離三十歲還有幾年，但也許她對這個年齡界限近自己而到焦慮。

似乎不大可能，他又漫無邊際地想了其他幾種可能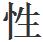。她會不會對學術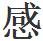到愈來愈悲觀？是對自己的研究過於專業化而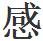到悲哀嗎？再不然，純悴是對自己的工作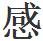到厭倦了嗎？

卡爾並不相信這些焦慮是雷內行為古怪的原因。果真是這樣的話，他覺得自己肯定會發現蛛絲馬跡。但他現在得到的印象卻全然不是這麼回事。令雷內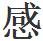到苦惱的無論是什麼，反正他猜不透。這使他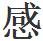到煩惱。

61931年，庫特哥德爾⑥證明了兩大定理。第一個定理實際上表明:數學包含或許是真實的、但在本質上卻無法證明的陳述。甚至簡單如算術的形式系統也可以包括確，有意義，而且似乎真實無疑的陳述，但卻無法用形式方法加以證明。

他的第二個定理表明:斷言算術具有邏輯上的一致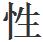，這就是上面所說的那種陳述之一，採用算術公理的任何方法都不能證明其真實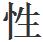。也就是說，作為一種形式系統的算術無法保證不會得出1=2這樣的結果。這樣的矛盾也許永遠不會遇到，但卻無法證明絕對不會遇到。

6a卡爾再次走進雷內的書房。她站在書桌跟前，抬頭看他。他鼓起勇氣說:雷內，顯然是她打斷她的話，你想知道我煩惱的原因嗎？好吧，我告訴你。說著雷內便拿出一張白紙，坐在書桌跟前，等一下，這需要一點時間。卡爾又張開嘴，但雷內揮手示意他保持沉默。接著，她深深地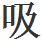了一口氣，開始寫起來。

她畫了一條線，穿過紙的中央，將紙分成兩欄。然後，她在一行的頂部寫下數字1，另一行的頂部寫下數字2。接著在這兩個數字下面迅速潦草地畫一些符號，又在這些符號下面的行列裡把它們擴展成一串串別的符號。她邊寫邊咬牙切齒，寫下那些文字時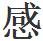，覺好像她正用指甲刮過黑板似的。

寫到紙的三分之二左右時，雷內開始將長串長串的符號減少成連續的短串符號。她心裡想，現在要到關鍵處了。她意識到自己在紙上用力過重了，下意識地放鬆握在手中的鉛筆。在她下面寫出的那一行上，符號串變成相等了。接著，她重重地寫了個=號，橫過紙的底部中心線。

她將紙遞給卡爾。他望著她，表示看不懂。看一看頂部吧。他照辦了，再看一看底部。

他眉頭緊鎖。我還是看不懂。

我發現了一種體系，可以使任何數字等於任何別的數字。這張紙上就證明了一和二是相等的。你隨便挑兩個數字，我都可以證明它們是相等的。

卡爾似乎竭力在回憶什麼。裡面肯定出現了以零為被除數的情況，對嗎？

不對。沒有不符合規則的運算，沒有不嚴謹的術語，沒有想當然假定的獨立公理，全都沒有。證明過程絕對沒有采用任何規則止的東西。

卡爾搖了搖頭。等一下。顯然一和二是不相等的。

但在形式上它們是相等的:證明就在你手裡。我使用的一切方法都是絕對無可爭議的。

但這兒不就是矛盾嗎？

說對了。也就是說，算術作為一種形式系統，是不一致的。

6b你找不出錯誤來，這就是你的意思嗎？

不對，你沒有聽。你以為我是因為這種情況才焦頭爛額的嗎？證明本身並沒有錯誤。

你的意思是說，用的方法都是對的，結果卻出了錯？

正確。

你肯定他戛然而止，卻太晚了。她瞪著他。她當然清楚他想說的是什麼。不知她的目光是什麼意思。