卷十三

如果出现文字缺失，格式混乱请取消转码/退出阅读模式

求朔弦望經辰所入因天正經辰所入餘奇，加七、餘五百一十二、奇九。奇滿率成餘。餘，如總法為，得上弦經辰所入。以次轉加，得望、下弦及來月朔。所入滿變及餘奇，則去之。凡相連去者，皆仿於此。徑求望者，加朔所入十四、餘一千二十五、奇六。徑求次朔，加一、餘一千三百七、奇十一。

求朔望弦盈朒減辰所入術各以其所入盈朒定積，盈加朒減其恆經辰所入，餘即各所求。

求朔弦望盈朒辰入變遲速定數術各列其所入增減率，並後率而半之，為通率。又二率相減，餘為率差。增者，以入餘減總法，餘乘率差，總法而一，並率差而半之。減者，半入餘乘率差，亦總法而一，並以加於通率，入餘乘之，總法而一，所得為經辰變轉半經辰變。速減遲加盈朒經辰所入餘，為轉餘。應增者，減法。應減者，因餘。皆以乘率差，總法而一，加於通率。變率乘之，總法而一，以速減遲加變率為定率。乃以定率增減遲速積為定。此法微密至當，以示算理通途。若非朔望有及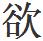考校速要者，但以入餘乘增減率，總法而一，增減速為要耳。其後無同率者，亦因前率，應增者以通率為初數，半率差而減之；應減入餘進退者分為二，隨餘初末，如法求之。所得並以加減變率為定。

其入前件餘，如初數已下者為初，已上者以初數減總法，餘為末之數。增減相反，約以九分為限。初雖少弱，而末微強，餘差不多，理況兼舉，皆今有雜差，各隨其數。若恆算所求，七與二十一得初率，而末之所減，隱而不顯。且數與平行正算，亦初末有數，而恆算所無。其十四、二十八既初末數存，而虛差亦減其數，數當去恆法不見。

求朔弦望盈朒所入名及小餘術各以其所入變歷速定數速減遲加其盈朒小餘。滿若不足，進退其。命以甲子算外，各其盈朒反餘。加其恆，餘者為盈；減其恆，餘者為朒。其不動者，依恆朔而定其小餘，推擬月行度。其定小餘二十四已下，一千三百一十六已上者，其入氣盈朒、入歷遲速，皆須覆依本術推算，不得從舉速要之限。乃前朔後朔，迭相推校。盈朒之課，據實為準。損不侵朒，益不過盈。

求定朔月大小術凡朔盈朒名，即為定朔名。其定朔名，十干與來月同者大，不同者小。其月無中氣者為閏月。其正月朔有定加時正月者，消息前後各一兩月，以定月之大小。合虧在晦二者，弦望亦隨事消息。凡置月朔，盈朒之極，不過頻三。其或過者，觀定小餘近夜半者量之。

檢宿度術前件周天二十八宿，相距三百六十五度，前漢唐都以渾儀赤道所量。其數常定，紘帶天中，儀圖所準。月往來，隨損益。所入宿度，進退不同。

黃道宿度左中郎將賈達檢月所去赤道不同，更鑄黃道渾儀所檢者。

臣等今所修撰討論，更造木渾圖絡調賦黃赤二道三百六十五度有奇，校量大率，與此符會。今歷以步行月及五星出入循此。其月行絡黃道，進退亦宜有別。每輒差，不可詳盡。今亦依黃道推步。

推躔術置冬至初躔差率，加總法，乘冬至小餘，如總法而一，以減天宿度分。其餘命起黃道鬥十二度，宿次去之，經鬥去宿分度，不滿宿算外，即所求年冬至夜半所在宿度算及分。

求每定氣初夜半所在定度術各以其定氣初躔差率，乘氣定餘，總法而一，進加退減餘為分，以減定氣度及分，命以宿次如前，即其夜半度及秋二分定氣初為進退之始，當平行一度。自餘依進加退減度之。

求次夜半所在定度術各因定氣夜半所在為本，加度一。又以其躔差率，進加退減度分。滿若不足，並依前例。去命如上，即得所求。其定朔弦望夜半度，各隨定氣，以其月名亦直而分別之。勘右依恆有餘，從定恆行度，不用躔差。

求朔弦望定夜辰所加度術各以其定小餘為平分。又定小餘乘其所躔差率，總法而一，乃進加退減其平分，以加其夜半度，即各定辰所加。其與五星加減者，半其分，消息月朔者，應推月度所須，皆依本朔大小。若注歷，依甲子乙丑各擬入。

推月離術求朔望定辰月所在度術各置朔弦望定辰所加度及分。

凡朔定辰所加為合朔，月同度。上弦加度九十一、分四百一十七。

望加度一百八十三、分八百三十四。

下弦加度二百七十三、分一千二百五十一。訖，各半而十退之，為程度分。

求次月定朔夜半入變歷術置天正恆朔夜半所入變及餘。定朔有進退一者，進退一，為定朔夜半所入。

月大加二，月小加一。餘皆五百九十六、奇十六。

求次夜半所入變歷術因定朔夜半所入算，加一，滿皆如前。其弦皆依前定所在求之。

求變定離程術各以其夜半入變餘，乘離差，總法而一，為見差。以進加退減其離程，為月每所離定程。

求朔弦望之定夜半月所在度術各以其定小餘，乘所入變離定程，總法而一，為夜半後分。滿程法為度，餘為度分。以減其加辰所在度及分，命以黃道宿度，即其所求。次夜半，各以離定程加朔弦望夜半所在分，滿程法從度，去命以黃道宿度算外，則次夜半月度。求晨昏度，以其離定程乘其夜刻，二百而一，為昏分，滿程法為度。望前以昏，後以晨，加夜半度，得所求。其弦望以五乘定小餘，程法一，為刻，即各其辰所入刻數。皆減其晨前刻，不盡為晨後刻。不滿晨前刻者，從前注歷，伺候推。

總刻:一百。辰刻:分十一。刻分法:七十二。

求定氣晝夜漏刻及出沒術倍其氣晨前刻及分，滿法從刻，為不見漏。以減百刻，餘為見漏。五刻晝漏刻。以晝漏刻減百刻，餘夜漏刻。以四刻十二分加晨前漏刻，命起子初刻算外，即出辰刻。以見漏加出刻辰，以次如前，即沒所在辰刻。以二十五除從夜漏，得每更一籌之數。以二刻三十六分加沒辰刻，即甲辰刻，又以更籌數加之，得甲夜一籌數。以次累加，滿辰去命之，即五更夜籌所以當辰刻及也，以配二十一箭漏之法也。

求每並屈申數術每氣準為一十五，各置其氣屈申率。每以發斂差損益之，差滿十從分，分滿十從率一，即各每屈申率。各累計屈申率為刻分，乃以一百八十乘刻分，泛差十一乘綱紀而除之，得為刻差，滿法為刻。隨氣所在，以申減屈加不見漏而半之，為晨前定刻。每求次，各如前法。時加其如始，隨加辰晚，以率課之。

求黃道去極每差術置刻差，三十而一為度。不滿三約為分。申減屈加其氣初黃道度，即每所求。

求昏旦去中星度術每求其晝漏刻數，以乘期實，二百乘總法而除之，得昏去中星度。以減周天度，餘為晨去中星度。以昏旦去中星度，加其辰所在，即各其中宿度。其梗概舉者，加其夜半度，各其中星宿度。

因求次者，各置其四刻差，七十二乘之，二百八十八而一度。冬至後加，夏至後減。隨加，各得每去中度。晨昏所距在黃道中星準度，以赤道計之。其赤道同太初星距。

推遊術終率:一千九十三萬九千三百一十三。奇率:三百。

約終:三萬六千四百六十四奇一百一十三。