卷十四

如果出现文字缺失，格式混乱请取消转码/退出阅读模式

辰星终率:三十五万二千二百七十九；秒，七十二。

终:一百一十五；馀，二千六百七十九；秒，七十二。

中合:五十七；馀，二千八百五十九；秒，八十六。

变差算:空；馀，一百三十六；秒，七十八六十。

象算:九十一；馀，二百四十四；秒，九十八六十。

爻算:十五；馀，一百六十七；秒，三十九七十四。

辰法:七百六十。

秒法:一百。

微分法:九十六。

推五星平合置中积分，以天正冬至小馀减之，各以其星终率去之，不尽者，返以减终率，大衍通法为，不为馀，即所求年天正冬至夜半后星平合算及馀秒也。

求平合入爻象历置积年，各以其星变以差乘之，乾实去之，不者，以大衍通法约之，为。不尽为馀秒。以减其星冬至夜半后平合算及馀秒，即平合入历算数及馀秒也。各四约其馀，同其辰法也。

求平合入四象置历算数及秒，以一象之算及馀秒除之，所得，依入爻象次命起少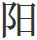算外，即平合所入象算数及馀秒也。

求平合入六爻置所入象算数及馀秒，以一爻之算及馀秒除之，所得，命起其象初爻算外，即平合所入爻算数及馀秒也。

求四象六爻每算损益及进退定数以所入爻与后爻损益率相减为前差，又以后爻与次后爻损益率相减为后差，前后差相减为中差。置所入爻并后爻损益率，半中差以加之，九之，二百七十四而一，为爻末率，因为后爻初率。皆因前爻末率，以为后爻初率。初末之率相减，为爻差。倍爻差，九之，二百七十四而一为算差。半之，加减初末，各为定率。以算差累加减爻初定率，少象以差减，老象以差加。为每损益率。循累其率，随所入爻，损益其下进退，即各得其算定。其四象初爻无初率，上爻无末率，皆置本爻损益，四而九之，二百七十四而一，各以初末率减之，皆互得其率。馀依术算，各得所求。

求平合入进退定数各置其星平合所入爻之算差，半之，以减其所入算损益率。损者，以所入馀乘限差，辰法除，并差而半之；益者，半入馀乘差，亦辰法除。加所减之率，乃以入馀乘之，辰法而一，所得以损益其算下进退，各为平合所入进退定数。此法微密，用算稍繁。若从省求之，亦可置其所入算馀，以乘其下损益率，如辰法而一，所得以损益其算下进退，各为定数。

求常合置平合所入进退定数，金星则倍置之。各以合下乘数乘之，除数除之，所得辰法为，不为馀，以进加退减平合算及馀秒，先以四约平合馀，然以进加退减也。即为冬至夜半后常合算及馀也。

求定合置常合先后定数，四而一，所得辰法为，不为馀。乃以先减后加常合算及馀，即为冬至夜半后定合算及馀也。

求定合度置其盈缩分，四而一以定合馀乘之，辰法而一，所得以盈加缩减其定馀，以加其夜半度馀，先四约夜半度馀以加之。辰法从度。依前命之算外，即为定合加时度及馀也。

求定合月置冬至夜半后定合算及馀秒，以天正冬至大小馀加之，天正经朔大小馀减之。其至、朔小馀，皆以四约之，然用加减。若至大馀少于经朔大馀者，又以爻数加之，然以经朔大小馀减之。其馀四象之策及馀，除之，为月数，不尽者，为入朔算及馀。命月数起天正算起经朔算外，即定所在月也。其定朔大馀有进退，进减退加一，为在其月定及馀也。

求定合入爻置常合及定合应加减定数，同名相从，异名相消。乃以加减其平合入爻算馀，若不足，进退其算，即为定合入爻算数及馀也。

求变行初入爻置定合入爻算数及馀，以合后伏下变行度常率加之，爻率去之，命爻次如前，即次变初入爻算数及馀也。更求次变入爻变入，但以其下行度常加之，去命如上节。

求变行初入进退定数各置其变行初入爻算数及馀，如平合求进退术入之，即得变行初所入进退定数也。置进退定数，各以其下乘数乘之，除数除之，所得各为进退变率。

求变行度率置其本进退变率与后变率，同名者，相消为差。在进前少，在退前多，各以差为加；在进前多，在退前少，各以差为减。异名者，相从谓并。前退后进，各以并为加；前进后退，各以并为减。逆行度率则反之。皆以差及并，加减度中率，各为度变率。其水星疾行，直以差以并加减度之中率，为变率。其直因中率为变率，不烦加减也。

求变行度定率以定合与后变初先后定数，同名相消为差，异名者相从为并。四而一，所得辰法为度。乃以盈加缩减其合后伏度之变率及合前伏之变率。金水夕合度，加减反之。其二留之变率，若差于中率者，即以所差之数为度，各加减本迟度之变率。谓以多于中率之数加之，少于中率之数减之。以下加减准此。退行度变率，若差于中率者，即倍所差之数，各加减本疾度之变率。其木土二星，既无迟疾，即加减前后顺行度之变率。其水星疾行度之变率，若差于中率者，即以所差之数为，各加减留变率。其留变率若少不足减者，即侵减迟变率也。各加减变率讫，皆为度定率。其定率有分者，前后辈之。辈，配也。以少分配多分，全为，有馀转配。其诸变率不加减者，皆依变率为定率。

求定合后夜半星所在度置其星定合馀，以减辰法，馀以其星初行分乘之，辰法而一，以加定合加时度馀，辰法为度。依前命之算外，即定合后夜半星所在宿及馀。自此以后，各依其星，计行度所至，皆从夜半为始也。转求次夜半星行至:各以其星一所行度分，顺加退减之。其行有小分者，各其法从行分一。行分辰法，从度一。合之前后，伏不注度，留者因前，退则依减。顺行出虚，去六虚之差；退行入虚，先加此差。先置六虚之差，四而一，然用加减。讫，皆以转法约行分为度分，各得每所至。其三星之行度定率，或加或减，益疾益迟，每渐差，难为预定，今且略据度中率商量置之。其定率既有盈缩，即差数合随而增损，当先检括诸变定率与中率相近者，因用其差，求其初末之行分为主。自馀变因此消息，加减其差，各求初末行分。循环比校，使际会参合，衰杀相循。其金水皆以平行为主，前后诸变，亦准此求之。其合前伏虽有度定率，如至合而与后算计却不叶者，皆从后算为定。其五星初见伏之度，去不等，各以度与星度相校。木去十四度，金十一度，火土水各十七度，皆见；各减一度皆伏。其木火土三星前顺之初，后顺之末，又金水疾行、留、退初末，皆是见伏之初，注历消息定之。其金水及月等度，并弃其分也。

求每差置所差分为实，以所差为法。实如法而一，所得为行分，不尽者为小分。即是也每差所行分及小分也。其差若全，不用此术。

求平行度及分置度定率，以辰法乘之，有分者从之，如定率而一，为平行分。不尽，为小分。其行分辰法为度，即是一所行度及分。

求差行初末行度及分置定率减一，以差分乘之。二而一，为差率，以加减平行分。益疾者，以差率减平为初，加平为末。益迟者，以差率加平为初，减平为末也。加减讫，即是初末所行度及分。其差不全而与相合者，先置定率减一，以所差分乘之，为实。倍所差为法。实如法而一，为行分。不尽者，因为小分，然为差率。

求差行次行度及分置初行分，益迟者，以每差减之；益疾者，以每差加之，即为次行度及分也。其每差、初行皆有小分，母既不同，当令同之。然用加减，转求次，准此各得所求也。

径求差行馀行度及分置所求减一，以每差乘之，以加减初行分，益迟减之，益疾加之。辰法为度，不为行分，即是所求行度及分也。

求差行，先定数，径求积度及分置所求减一，次每差乘之，二而一，所得，以加减初行分。益迟减之，益疾加之。以所求乘之，如辰法而一，为积度。不尽者，为行分。即是从初至所求积度及分也。

求差行，先定度数，径求数置所求行度，以辰法乘之，有分者从之。八之，如每差而一，为积。倍初行分，以每差加减之。益迟者加之，益疾者减之。如每差而一，为率。今自乘，以积加减之，益迟者以积减之，益疾者以积加之。开方除之。所得，以率加减之。益迟者以率加之，益疾者以率减之。乃半之，即所求数也。其开方除者，置所开之数为实，借一算于实之下，名曰下法。步之，超一位，置商于上方，副商于下法之上，名曰方法。命上商以除实，毕，倍方法一折，下法再折，乃置后商于下法之上，名曰隅法。副隅并方，命后商以除实，毕，隅从方法折下就除，如前开之。讫除，依上术求之即得也。

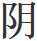
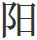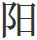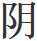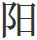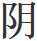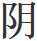
求星行黄道南北各视其星变行入爻而定之。其前变入爻为黄道北，入爻为黄道南；后变入爻为黄道南，入爻为黄道北。其金水二星，以爻变为前变，各计其变行，起初入爻之算，尽老象上爻末算之数，不变行度常率者，因置其数，以变行定率乘之，如变行度常率而一，为。其入变数，与此数以下者，星在黄道南北，依本所入爻为定。过此数之外者，黄道南北则返之。