第230章

如果出现文字缺失，格式混乱请取消转码/退出阅读模式

……

一個數學猜想的解決，需要的是工作量的累計，以及一位富有創造力的天才。

兩者缺一不可。

就像費馬大定理。

當谷山志村猜想被證明後，儘管人們還看不到具體的前景，但所有的人心中都有數了，因為一個可以解決問題的工具已經出現了。果然，安德魯·懷爾斯，最終完成了這一歷史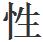的工作。

但對於哥德巴赫猜想而言，無論是大篩法還是圓法，都差一點這種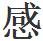覺。

前人的工作做了很多鋪墊，但無論是從“9+9”到“1+2”的陳氏定理，還是赫爾夫戈特對奇數條件下哥德巴赫弱猜想的證明，都只差最後一步。甚至於陳氏定理的意義，更多的是讓其它數學家瞭解到，大篩法這條路已經被陳景潤做到了極致，這條路已經走不通了。

圓法也是一樣。

也正是因為同樣的理由，在去年年終的演講上，赫爾夫戈特才用“關於完全證明哥德巴赫猜想，我們還有很長的路要走”作為最後的結束語，表達自己對短期內解決不了巴赫猜想不抱希望。

至少，對圓法不抱希望。

陸舟不開始反思，是不是這兩種方法都走進了死衚衕。

他當初研究孿生素數猜想時，也面臨過類似的問題。

張益唐的研究通過巧妙地選取選取了lambda函數，將素數對的間距限定在了七千萬，後繼者在一年之內將這個數字縮小到了246，然後便無法寸進一步。

陸舟最初的思路也是選取一個恰當的lambda函數，但經過了無數次的嘗試之後，最終還是發現這條路走不通。

可以選擇的lambda函數實在是太多了，但無論他如何尋找，都找不到恰到好處的那一個。

直到，他在啟發狀態下，嘗試了一條截然不同的證明思路，將拓撲學理論引入到了篩法的概念中，才打開了新世界的大門。

雖然這條思路是澤爾貝格教授95年那篇關於哥德巴赫猜想研究的論文中最先提到的，但對它加以改進並引入到素數對問題中的卻是他自己。

再到後來陸舟在此基礎上引入了群論的知識，將有限距離的素數對推到無限，在此基礎上解決了波利尼亞克猜想，這種方法已經被兩次魔改改造的面目全非，完全偏離了篩法的原貌。

因此陸舟給這把屬於自己的武器刻上了一個新的名字，即“群構法”。

但是在思考哥德巴赫猜想的時候，慣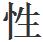思維卻讓他選擇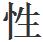地忽略掉了自己的工具。

表面上看群構法似乎和哥德巴赫猜想沒有任何關係，但從源上它正是從篩法演變而來，並且始終為解決素數問題而去。

只要加改進，未必不可以將這項工具，用於同為素數問題的哥德巴赫猜想上。

當這種數學方法被不斷的完善，完善到足以解決很多問題，完善到從牙籤變成了瑞士軍刀，它的意義可能便不再是一種單純工具，而是逐漸演變成一種理論框架！而且是解析數論中的理論框架！

就像數學界有名的“中二病”望月新一，在研究ABC猜想時創造的“宇宙際Teichmüller理論”和“外星算數全純結構”一樣。

無論是先建立理論再去證明理論的價值，還是在研究具體數學問題的同時發展出新穎的理論，都是有先例可循的。

從哥德巴赫猜想中，陸舟隱約看到了希望。……從飲食俱樂部出來之後，陸舟沒有像往常一樣，吃完飯後去圖書館待一會兒，而是去了普林斯頓高等研究所。

雖然他並沒有預約，但據德林教授自己的說法，不出意外的話，每天晚上6點到8點的這段時間裡他都會在這裡。

敲開辦公室的門，陸舟走了進去。

停下了手中的圓珠筆，德利涅教授看向了站在辦公桌對面的陸舟，語氣輕鬆的問道。

“你已經考慮好了？”陸舟點了點頭，說道。