(264-265)
如果出现文字缺失,格式混乱请取消转码/退出阅读模式
2019-04-05【第二百六十四章算學寶鑑】在程澧一陣掐人中
 口的急救下,王文素悠悠醒轉。
口的急救下,王文素悠悠醒轉。
看着眼前一臉憂 的二人,王文素赧顏道:「在下一時失態,煩勞二位了。」
的二人,王文素赧顏道:「在下一時失態,煩勞二位了。」
「尚彬,你可是有何隱疾,直説無妨,府內有太醫院名醫坐診,庫房也不乏珍稀藥材,保你無恙。」丁壽憂心忡忡,這哥們別有什麼傳染病,府上這麼多女人,萬一哪個倒黴過了病氣,再湊巧和二爺發生些「深入溝通」,不是把自己給坑了麼。
王文素聽了丁壽關切問話,熱淚滾滾,哽咽道:「小人何德何能,得大人如此垂青,士為知己者死,小人願憑此殘軀,供大人驅使,若違此言,天人公憤!!」丁壽 本就不把誓言當回事,只是一再確認王文素是不是身體有恙,當最後確定王先生只是一時
本就不把誓言當回事,只是一再確認王文素是不是身體有恙,當最後確定王先生只是一時 動過度後,才算鬆了口氣。
動過度後,才算鬆了口氣。
「老王啊,你就這點出息!」既然人家賭咒發誓投效了,丁壽也就不再客氣見外。
王文素臉上有些發燒,「是,小人眼界淺,沒見過什麼世面,教大人見笑了。」
「説了半天,你那書叫什麼名字?」丁壽從果盤中拿了個桃子,一上一下地拋個不停。
「説來慚愧,小人妄想集採古今算學之長,故 取名《新集通證古今算學寶鑑》,書尚未完稿,暫稱《算學寶鑑》……」
取名《新集通證古今算學寶鑑》,書尚未完稿,暫稱《算學寶鑑》……」
「《算學寶鑑》?!」丁壽不由愣了,一時忘了去接從空中落下的桃子,結果攜着重力加速度的那顆大黃桃,正中二爺襠下要害。
「喲,爺,怎麼了這是?」程澧一個箭步衝過去,扶住跳腳亂蹦的丁二。
怎麼了?早説王文素這個名字耳 ,一直沒想起來,原來是寫《算學寶鑑》的這位呀!丁壽記憶裏前世看過一篇文章,便是介紹《算學寶鑑》的。
,一直沒想起來,原來是寫《算學寶鑑》的這位呀!丁壽記憶裏前世看過一篇文章,便是介紹《算學寶鑑》的。
和現代人想的古人不重視數學不同,數學早就是周禮「六藝」之一,古代數學更是文明璀璨,成就頗多,《易經》、《河圖》、《洛書》、《山海經》、《周髀算經》等先秦著作今人也無法完全理解。
先秦時的《周髀算經》中,有關於如何計算地球到太陽距離以及計算地球周長的方法和記錄,記載了勾股定理, 象的説明了直角三角形的直角邊平方和等於斜邊平方和,而且還給出了完整的證明過程,比之古希臘的畢達哥拉斯要早數百年,其他至於二進制、十進制、球座標系、
象的説明了直角三角形的直角邊平方和等於斜邊平方和,而且還給出了完整的證明過程,比之古希臘的畢達哥拉斯要早數百年,其他至於二進制、十進制、球座標系、 影幾何、割圓術、地動學等知識均有記述,而所謂的
影幾何、割圓術、地動學等知識均有記述,而所謂的 耳曼人,當時還在原始森林裏光着
耳曼人,當時還在原始森林裏光着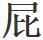 股打獵玩呢。
股打獵玩呢。
犬戎攻滅西周,大量典籍損失,只有殘篇碎語,經 秋戰國西漢等數代整理,才得面世,在東漢初年出現的《九章算術》,主要是應用數學,教大家如何計算土地的面積等等,同時也對勾股定理作了進一步的發展。
秋戰國西漢等數代整理,才得面世,在東漢初年出現的《九章算術》,主要是應用數學,教大家如何計算土地的面積等等,同時也對勾股定理作了進一步的發展。
魏晉時期的數學家劉徽為《九章算術》作注,把《九章算術》裏面的算法進行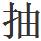 象化總結,建立了一套從概念到定理的系統化的數學理論,這是中國數學思想史上的一次大飛躍。
象化總結,建立了一套從概念到定理的系統化的數學理論,這是中國數學思想史上的一次大飛躍。
南朝祖沖之在劉徽開創的探索圓周率的 確方法的基礎上,首次將「圓周率」
確方法的基礎上,首次將「圓周率」 算到小數第七位,直到16世紀,這一紀錄才被阿拉伯數學家阿爾•卡西才打破。可人家祖沖之不僅是算了個圓周率,他的《綴術》理論十分深奧,計算相當
算到小數第七位,直到16世紀,這一紀錄才被阿拉伯數學家阿爾•卡西才打破。可人家祖沖之不僅是算了個圓周率,他的《綴術》理論十分深奧,計算相當 密,對立體幾何和三次方程求解正
密,對立體幾何和三次方程求解正 的問題進行了深入的研究。這些都是處在當時世界最領先地位的數學研究。
的問題進行了深入的研究。這些都是處在當時世界最領先地位的數學研究。
隋唐雖把祖沖之的《綴術》列入官方數學教材,但「祖沖之所著之書,名為綴術。學官莫能究其深奧,故廢而不理。」《綴術》最後失傳了。
一直過了六百年,到了南宋後期,中國的數學研究才又達到了一個新的高峯。以秦九韶和元初朱世傑為代表的數學家,提出了多元高次方程組的建立和求解方法,研究了高階等差級數的計算,證明了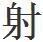 影定理和絃冪定理等等。崖山之後,高峯再斷。
影定理和絃冪定理等等。崖山之後,高峯再斷。
現代許多學者認為明代是古代數學的沉寂和倒退期,例如前代的增乘開方和天元術在明代失傳等等理由,而打臉他們的便是民國期間重被發現的《算學寶鑑》,書中研究了一元高次方程的數值解法,內容詳實可貴,這充分説明一元高次方程數值解法及天元術、四元術在明朝並未完全失傳。
王文素在解法中所用名詞術語、演算程序,基本上與宋元數學一致,並有所發展和創新,其解高次方程的方法較英國的霍納、意大利的魯非尼早200多年。在解代數方程上,他走在牛頓、拉夫森的前面140多年。對於17世紀微積分創立時期出現的導數,王文素在16世紀已率先發現並使用。
《算學寶鑑》中的「開方本源圖」獨具中國古代數學傳統特 ,國外類似的圖首見於法國數學家斯蒂非爾1544年著的《整數算術》一書,較《算學寶鑑》遲20年且不夠完備。中國古代數學中的縱橫圖在現代計算機技術上得到應用,王文素書中縱橫圖比之宋楊輝在深度和廣度上都有了很大進步和提高。
,國外類似的圖首見於法國數學家斯蒂非爾1544年著的《整數算術》一書,較《算學寶鑑》遲20年且不夠完備。中國古代數學中的縱橫圖在現代計算機技術上得到應用,王文素書中縱橫圖比之宋楊輝在深度和廣度上都有了很大進步和提高。
其實即便拋開王文素,明代數學也非一無是處,明代數學與前代不同在於其時發生了一場算學革命。
某些穿越者一回古代便喜歡拋出阿拉伯數字,顯示其算學高明,許多皓首窮經的算學大家倒頭就拜,奉為神明,暫且不説某人在穿越時究竟如何的數學水平,那個原產天竺的阿拉伯數字老早便已傳入中國,只不過古代中國人更喜歡用算籌,而且千年積累,早已成就了一套完備的知識體系,那玩意在中國就不受人待見。
其實這還算好的,要是有哪位神經大條的穿越者把阿拉伯數字獻給洪武皇帝,怕是當時就得被砍了頭,洪武四大案中的「郭桓案」便是上下勾結塗改賬冊,朱八八以此為鑑,完善推廣大寫數字,將「一、二、三、四、五、六、七、八、九、十、百、千」改為「壹、貳、叁、肆、伍、陸、柒、捌、玖、拾、佰(陌)、仟(阡)」,沿用至今,你小子呈獻的這七拐八拐的回回數字更容易篡改,你丫安的什麼心!
籌算有優點,自然也有缺點,計算得越複雜,所需要的面積就越大,而明朝民間商業 趨繁榮,需要計算之處太多,所以更加方便的算盤和珠算開始取代算籌與籌算。
趨繁榮,需要計算之處太多,所以更加方便的算盤和珠算開始取代算籌與籌算。
1450年吳敬的《九章算法比類大全》、1573年徐心魯的《盤珠算法》,1578年柯尚遷的《數學通軌》,1584年朱載堉的《算學新説》,1592年程大位的《算法統宗》,以及1604年黃龍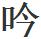 的《算法指南》,無一例外多是由籌算向珠算過渡並深入研究的著作。
的《算法指南》,無一例外多是由籌算向珠算過渡並深入研究的著作。
珠算算法沒有發展到前人的籌算高度成果也不是時人輕視,君不見作者裏還有一位天潢真人。中國數學從元朝末期開始,一直是沿着實用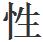 、技巧
、技巧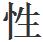 的方向發展,這與偏向演繹、
的方向發展,這與偏向演繹、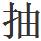 象的古希臘數學不同。珠算作為一種傳統數學機械化算法體系的應用,滿足了明代社會需要,適應了商業發展的要求,代替籌算大勢所趨,但因為工具
象的古希臘數學不同。珠算作為一種傳統數學機械化算法體系的應用,滿足了明代社會需要,適應了商業發展的要求,代替籌算大勢所趨,但因為工具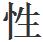 能的限制,無法複製千百年來籌算積累的研究成果,還需進一步完善體系,這都需要時間積累。
能的限制,無法複製千百年來籌算積累的研究成果,還需進一步完善體系,這都需要時間積累。
古希臘文明覆滅以後一千多年,歐幾里得的《幾何原本》再次被阿拉伯人發揚光大,而歐洲人在古希臘數學成就的基礎上發展出近代數學,則距離《幾何原本》的成書年代相隔了最少一千五百年,明代雖然經濟高度繁榮,在一些材料類、工程類方面的科學技術成就也很多,但數學理論要想再次達到新的高度,正常發展下去,也至少還再需要兩百年。
15世紀歐洲開始文藝復興,大航海時代到來,商業的繁榮同樣刺 了歐洲數學的發展,主要集中在算術、代數與三角學領域,同樣著作不斷,將15、16世紀中西方同期數學進行評判,整體數學水平相當,商業數學發展是其共
了歐洲數學的發展,主要集中在算術、代數與三角學領域,同樣著作不斷,將15、16世紀中西方同期數學進行評判,整體數學水平相當,商業數學發展是其共 ,明代數學在算盤應用、算法口訣及珠算的普及度遠遠超過歐洲,而西方數學中符號系統與公理化演繹體系則為中算所不及。
,明代數學在算盤應用、算法口訣及珠算的普及度遠遠超過歐洲,而西方數學中符號系統與公理化演繹體系則為中算所不及。
明朝末年,西方數學開始傳入中國。徐光啓翻譯了歐幾里得《幾何原本》的前六卷,標誌着中國開始從傳統數學研究向學習西方近代數學轉型。