第7節
如果出现文字缺失,格式混乱请取消转码/退出阅读模式
素數是這樣的整數,它除了能表示為它自己和1的乘積以外,不能表示為任何其它兩個整數的乘積。例如,15=3×5,所以15不是素數;又如,12=6×2=4×3,所以12也不是素數。另一方面,13除了等於13×1以外,不能表示為其它任何兩個整數的乘積,所以13是一個素數。
有的數,如果單憑印象去捉摸,是無法確定它到底是不是素數的。有些數則可以馬上説出它不是素數。一個數,不管它有多大,只要它的個位數是2、4、5、6、8或0,就不可能是素數。此外,一個數的各位數字之和要是可以被3整除的話,它也不可能是素數。但如果它的個位數是1、3、7或9,而且它的各位數字之和不能被3整除,那麼,它就可能是素數(但也可能不是素數)。沒有任何現成的公式可以告訴你一個數到底是不是素數。你只能試試看能不能將這個數表示為兩個比它小的數的乘積。
找素數的一種方法是從2開始用“是則留下,不是則去掉”的方法把所有的數列出來(一直列到你不想再往下列為止,比方説,一直列到10000)。第一個數是2,它是一個素數,所以應當把它留下來,然後繼續往下數,每隔一個數刪去一個數,這樣就能把所有能被2整除、因而不是素數的數都去掉。在留下的最小的數當中,排在2後面的是3,這是第二個素數,因此應該把它留下,然後從它開始往後數,每隔兩個數刪去一個,這樣就能把所有能被3整除的數全都去掉。下一個未去掉的數是5,然後往後每隔4個數刪去一個,以除去所有能被5整除的數。再下一個數是7,往後每隔6個數刪去一個;再下一個數是11,往後每隔10個數刪一個;再下一個是13,往後每隔12個數刪一個。…就這樣依法做下去。
你也許會認為,照這樣刪下去,隨着刪去的數越來越多,最後將會出現這樣的情況;某一個數後面的數會統統被刪去因此在某一個最大的素數後面,再也不會有素數了。但是實際上,這樣的情況是不會出現的。不管你取的數是多大,百萬也好,萬萬也好,總還會有沒有被刪去的、比它大的素數。
事實上,早在公元前300年,希臘數學家歐幾里得就已證明過,不論你取的數是多大,肯定還會有比它大的素數,假設你取出前6個素數,並把它們乘在一起:2×3×5×7×11×13=30030,然後再加上1,得30031。這個數不能被2、3、5、7、11、13整除,因為除的結果,每次都會餘1。如果30031除了自己以外不能被任何數整除,它就是素數。如果能被其它數整除,那麼30031所分解成的幾個數,一定都大於13。事實上,30031=59×509。
對於前一百個、前一億個或前任意多個素數,都可以這樣做。如果算出了它們的乘積後再加上1,那麼,所得的數或者是一個素數,或者是比所列出的素數還要大的幾個素數的乘積。不論所取的數有多大,總有比它大的素數,因此,素數的數目是無限的。
隨着數的增大,我們會一次又一次地遇到兩個都是素數的相鄰奇數對,如5,7;11,13;17,19;29,31;41,43;等等。就數學家所能及的數來説,他們總是能找到這樣的素數對。這樣的素數對到底是不是有無限個呢?誰也不知道。數學家認為是無限的,但他們從來沒能證明它。這就是數學家為什麼對素數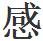 興趣的原因。素數為數學家提供了一些看起來很容易、但事實卻非常難以解決的問題,他們目前還沒能對付這個挑戰哩。
興趣的原因。素數為數學家提供了一些看起來很容易、但事實卻非常難以解決的問題,他們目前還沒能對付這個挑戰哩。
這個問題到底有什麼用處呢?它除了似乎可以增添一些趣味以外,什麼用處也沒有。
碧聲注:一點用處也沒有嗎?
…
聽説在密碼方面很有用哩。