第52節
如果出现文字缺失,格式混乱请取消转码/退出阅读模式
粒子以無限大的速度運動這種想法本身,看來似乎有一些荒謬的地方,它不需要花任何時間,就會從a點跑到b點,這就是説,它將不僅同時處在a點和b點上,而且也同時處在a、b兩點之間的各點上,它還會繼續跑到c、d、e等點上去,並且再進一步走過無限大的距離,而且這一切都不用花費任何時間。這樣一來,一個以無限大速度運動的粒子,就會具有一 無限長的固體
無限長的固體 的各種
的各種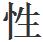 質。
質。
如果空間象愛因斯坦相對論所指出的那樣發生彎曲,那麼,這 固體
固體 實際上會成為一個巨大的圓或螺旋,要不然,就是某種形狀還要更加複雜的、變幻不定的曲線。
實際上會成為一個巨大的圓或螺旋,要不然,就是某種形狀還要更加複雜的、變幻不定的曲線。
不過,現在讓我們先來設想一個由快子構成的宇宙,在這個宇宙中,所有粒子的速度全都大於光速。當這種粒子所獲得的能量越來越多時,它們的運動速度就變得越來越慢,到它們得到無限大的能量時,它們的速度就降低到等於光速。當它們失去的能量越來越多時,它們就運動得越來越快,到它們的能量等於零的時候,它們的運動速度就達到無限大。
我們可以想象到,在這樣的宇宙中,粒子的能量範圍是很寬廣的:有些粒子的能量非常高,有些粒子的能量非常低,有些粒子的能量則介於這兩者之間(就象我們這個宇宙中粒子的實際情況那樣)。
在這樣的宇宙中(就象在我們這個宇宙中一樣),能量必須通過某種相互作用才能從一個粒子轉移給另一個粒子,比如説,要通過兩個粒子的碰撞,如果低能粒子a同高能粒子b發生碰撞,那麼,粒子a獲得能量而粒子b損失能量的機會是非常大的,所以,一般的趨勢是形成兩個具有中等能量的粒子。
當然,也會有一些例外的情形。如果是兩個能量相等的粒子發生相互作用,那麼,其中的一個粒子可能獲得能量,另一個粒子則損失能量,從而把能量範圍拉大了。甚至還有可能(儘管可能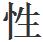 不大)發生這樣的情形:一個高能粒子通過同一個低能粒子相碰撞而獲得更多的能量,而那個低能粒子所剩下的能量卻比原來還要少。
不大)發生這樣的情形:一個高能粒子通過同一個低能粒子相碰撞而獲得更多的能量,而那個低能粒子所剩下的能量卻比原來還要少。
考慮到這種碰撞的隨機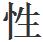 和能量轉移的隨機
和能量轉移的隨機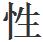 ,我們就會得出結論説,這些粒子的能量分佈必定是大多數粒子具有中等能量,有些粒子具有較高(或較低)的能量,少數粒子具有非常高(或非常低)的能量,非常少的粒子具有極高極高(或極低極低)的能量,只有痕量的粒子才具有極高極高極高(或極低極低極低)的能量。
,我們就會得出結論説,這些粒子的能量分佈必定是大多數粒子具有中等能量,有些粒子具有較高(或較低)的能量,少數粒子具有非常高(或非常低)的能量,非常少的粒子具有極高極高(或極低極低)的能量,只有痕量的粒子才具有極高極高極高(或極低極低極低)的能量。
在某一個範圍內的能量分佈可以用數學方法表示出來。並且我們會看到,實際上既沒有任何粒子具有無限大的能量,也沒有一個粒子的能量等於零,粒子只能非常接近這兩個能量值,但永遠不能達到它們。快子有時會以稍稍大於光速的速度運動,但它的速度永遠不會正好等於光速;快子也可能以確實非常巨大的速度運動,比光速還要快上百萬倍(或者上億倍或萬億倍),但它永遠不會達到真正是無限大的速度。
假定有兩個能量正好相同的快子非常準確地發生對頭碰撞。這時,它們的動能難道不會正好互相抵消掉,從而使兩者以真正無限大的速度離開碰撞地點而飛開嗎?這同樣是個只能 近而無法達到的想法。兩個快子具有正好相同的能量,並且非常準確地對頭碰撞的機會,那是小到等於零的。
近而無法達到的想法。兩個快子具有正好相同的能量,並且非常準確地對頭碰撞的機會,那是小到等於零的。
換句話説吧,在快子的宇宙中,真正無限大的速度是隻能 近、但無法達到的——在這種情況下,我們就不必去為無限大總是要引起的種種似乎荒謬絕倫的事情多傷腦筋了。
近、但無法達到的——在這種情況下,我們就不必去為無限大總是要引起的種種似乎荒謬絕倫的事情多傷腦筋了。