第42節

如果出现文字缺失，格式混乱请取消转码/退出阅读模式

當你第一次在愛因斯坦的相對論裏見到“彎曲空間”這個字眼時，恐怕是會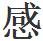到困惑的，真空怎麼能是彎曲的呢？你怎樣能使它彎曲起來呢？

為了明白這是怎麼一回事，先讓我們這樣想象:在一艘宇宙飛船裏，有人在仔細觀察附近的一顆行星。這顆行星的表面完全被深深的海洋覆蓋着，因此有着象枱球那樣的光滑表面。再假設有一條船在那個行星的海洋上沿赤道線朝正東方向行駛着。

現在再進一步設想一下，這位觀察者本看不見這顆行星，而只能看到這條船。當他研究這條船的運動路線時，他會驚訝地發現這條船走的是一條圓弧。它最後會回到自己的出發點，從而描繪出一個完整的圓周。

如果這條船改變路線，航道就會變得彎彎折折的，不再是個簡單的圓周。但是，不管它怎麼改道，無論它怎麼行進，它的航線總是在一個球面上。

據所有這些事實，這位觀察者可能會推斷出，這條船被束縛在一個看不見的球體的表面上，而束縛它的力正是指向球體中心的重力。要不，他就可能會認為，這條船被限制在一塊特殊的空間裏面。這塊空間是彎曲的，而且彎曲成一個球形，從而迫使這條船走出這樣的路線來。換句話説，我們必須在一個力和一種空間幾何形態之間作出選擇。

你大概會認為這是一種想象出來的局面，但實際上並非如此。地球這顆行星是沿着橢圓路線繞着太陽運行的，正象一條船在某個看不見的曲面上行駛一樣。至於這條橢圓路線，我們是假設太陽和地球之間有一種引力來解釋的，正是這種引力使地球保持在它的軌道上。

不過，我們也可以從空間幾何形態來考慮問題。我們不是通過觀察空間本身——空間是看不見的——而是通過考察物體在這種空間裏的運動方式，來確定這種空間的幾何形態。如果空間是“平坦的”各種物體就會走直線從這個空間中通過，如果空間是“彎曲的”各種物體就會走出彎曲的路線來。

一個具有確定質量和速度的物體，如果在離開其他質量都很遠的地方運動，那麼，它的路徑真的可以説是一條直線。而當它走近另一個質量的時候，它的路徑就會變得越來越彎曲，顯然，是質量把空間彎曲了。質量越大，離質量越近，空間彎曲的曲率就越大。

把萬有引力看作是一個力，看來要比用空間幾何形態去解釋它方便得多，也自然得多。但是，如果在考慮光的行進時，情形就會顛倒過來。按照比較舊的觀點，光是不受重力影響的，因為它沒有質量。然而，當光在彎曲空間裏穿過時，它的路徑也會彎曲起來。把光的速度考慮進來，它在太陽這個巨大質量的附近經過時路徑的彎曲就能計算出來了。

1919年，愛因斯坦的這一理論（發表於三年之前）在一次蝕期間受到了檢驗，人們把太陽位於空間某處時靠近太陽的某些恆星的位置，與太陽不在此處時這些恆星的位置進行了比較。結果，愛因斯坦的理論站住腳了。用彎曲空間來討論萬有引力，看來要比用力學術語更為確。

不過，我們還應該提一下，1967年，人們對太陽的形狀所進行的密測量，發現愛因斯坦的引力理論出了問題，今後將會發生些什麼情況？還得等着瞧。