第六百一十一章驚人的巧合

如果出现文字缺失，格式混乱请取消转码/退出阅读模式

題目紙落到地上，恰好，桌子的一角將一個三角形的陰影投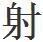其上，只出第一道題目的那一行小字。

字是仿宋體，用的是木版雕刻，很是美。雖然考舍光線昏暗，依舊能看得清楚。

卻見得第一題的題目霍然是:《牛山之木嘗美矣?》。

“這不就是真實歷史上弘治十六年會試時的題目嗎？”蘇木先前也是隻看了一眼，就驚得手一顫，將題目紙落到地上。

心臟也蓬蓬跳個不停，心有一個聲音在喊:“怎麼可能，怎麼可能。歷史明明已經改變了，而弘治十六年的會試不但沒有如期舉行。而且因為正德提前兩年登基，而順延一年，成為恩科加試。可為什麼，這第一場的第一題還是《牛山之木嘗美矣?》呢？”巧合，一定是巧合！

即便還沒有意識到這事究竟有什麼不同尋常之處，蘇木還是大覺鎮驚。

“是的，巧合。正如後世研究八股的導師説過，到清末時，科舉已經舉行了好幾百年。但八股題目又嚴格限制在《四書》《五經》幾本書的範圍之內。可以説，這幾本書的任何一個句子後面都有一大批優秀的八股跟着。”

“到最後，科舉‮試考‬的題目已經出無可出。出題人不得以，甚至出將兩個句子截頭去尾，拼湊在一起的咄咄怪事。這就是所謂的截塔題。”現在是明朝正德年間，截塔題這種怪胎還沒有出現在歷史上。

而且，《四書》《五經》的句子還沒有被出盡，而且，以朱熹的註解為審題標準也不過一百多年的時間，撞題的可能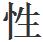實在不大。

所以，一看到這道題，蘇木就嚇了一跳。

呆呆地做了半天，他才深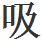了一口氣，俯下身去，將題目紙揀起來。

又朝第二題看去，這一看，又將他徹底驚住。

第二題正是:《孟子曰無傷也》“第三題應該是《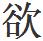齊其家者先修其身》了，會是嗎，會是嗎？連續兩到題目都全，這能夠用巧合來解釋嗎？”蘇木又看了一眼第三題。

沒錯，第三題和真實歷史上弘治十六年的會試題目一樣。

然後第四題和四道《五經》題目，也完全一樣。

燈光下，蘇木覺一股涼氣從腳底下升起，直衝腦門，身上也是一陣冰涼，不住微微顫抖起來。

而手上的題目紙也隨着自己的身形顫動着，扭曲着。

“啪嗒！”一滴水落到紙上，然後飛快的濡散開來。

然後是第二滴，第三滴。

這個時候，蘇木才發現自己額頭上全是黃豆大的汗水。

如果他面前放着一面鏡子的話，定然能夠看到一張畏懼的臉。

是的，蘇木畏懼了。

這種畏懼是對歷史巨大慣的畏懼。

自從蘇木穿越到明朝之後，因為他這隻蝴蝶的緣故，這片時空發生了巨大的改變。

首先，弘治皇帝就提前兩年去世，本應該弘治十七年變成了正德一年。歷史上那個温和寬容的張太后也因為經過一年垂簾聽政的鍛鍊，變成了一個出的女政治家。

至於弘治十六年的會試、殿試也延後一年成為正德一年的恩科。

可是，歷史的尊嚴不容挑戰。

就如同一條河，在遇到一個突然的波折之後，依舊依照他固有的慣迴歸本來的河道。歷史之所以成為歷史，一切歷史事件都有其必然的道理，非人力所能改變。

相比起真正的時空，蘇木這麼一個凡人卻是顯得如此的渺小。

也不過是一年時間，又開始慢慢地變成本來應該有的模樣。而這一切，就是從科舉開始的。

弘治十六年的會試題目再次出現。

想通這其的關節，蘇木被深深地震撼了:正德一年的會試題目要想和真實歷史上的弘治十六年完全一樣，從出題人的選擇，到最後皇帝抓鬮抓，充滿了無數的偶然，只需一個步驟出了岔子，就會變成另外一種模樣。偏偏這所有的偶然都被歷史這種看不見的巨手排除了，只剩下這唯一的必然。

“歷史，這是在複製弘治十六年的會試啊！”説句實在話，蘇木從來不認為自己和普通人有什麼不同。

在前世，他不過是一個尋常的大學老師。因此一種莫名其妙的原因穿越到明朝，附身在這個叫蘇木的人身上。

因為不甘於現狀，這才奮發讀書，通過科舉一路考上來，讓自己這一世的人生來了一個翻天覆地的變化。在他改變自己人生的同時，身邊和他相關的各人等的命運也徹底發生了變化。

最明顯的例子就是胡順因為有了自己的指點，從一個小小的百户軍官坐到了錦衣衞經歷司經歷的位置上，成為明朝特務機關的重要人物之一；而在屋裏躲了十年的老宅男吳世奇也獲得了正七品朝廷命官的官職。

這次有因為提前知道了第一場最重要的三道題，以他的學問，有很大可能考進士。

是的，據蘇木所知道。就在前一陣子，這個吳世奇就將這三道題目反反覆覆地寫了許多次，並選擇其最好的三篇早早地背了。正的一進考場，就直接謄錄在卷子上面。

老先生的章自不用説，那是極好的，這次又是有備而來，想不都難。

難怪剛才老先生一看到‮試考‬題目，就一副從容淡定的模樣，並心情愉快的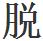衣上牀睡覺。

蘇木當初給他這三道題，不過是為了暫時哄住老先生，免得他突然發瘋。

在考前，他甚至還讓小蝶和吳小姐給吳世奇加大了藥量。

也因為這樣，老先生從昨天開始，就睡了整整一天一夜。

進考場，發題目紙的時候，蘇木還害怕老先生髮現題目不對後再次發瘋。

可現在…現在，任何人換成吳老先生，一看題目都對，不笑出聲來就算是修養技能樹點滿。

蘇木也是嘆息，想到不自己隨口將真實歷史上弘治十六年的題目説出來，竟然就説準了。

這個巧合也實在是太巧了點吧！