卷十三

如果出现文字缺失，格式混乱请取消转码/退出阅读模式

求朔弦望经辰所入因天正经辰所入馀奇，加七、馀五百一十二、奇九。奇率成馀。馀，如总法为，得上弦经辰所入。以次转加，得望、下弦及来月朔。所入变及馀奇，则去之。凡相连去者，皆仿于此。径求望者，加朔所入十四、馀一千二十五、奇六。径求次朔，加一、馀一千三百七、奇十一。

求朔望弦盈朒减辰所入术各以其所入盈朒定积，盈加朒减其恆经辰所入，馀即各所求。

求朔弦望盈朒辰入变迟速定数术各列其所入增减率，并后率而半之，为通率。又二率相减，馀为率差。增者，以入馀减总法，馀乘率差，总法而一，并率差而半之。减者，半入馀乘率差，亦总法而一，并以加于通率，入馀乘之，总法而一，所得为经辰变转半经辰变。速减迟加盈朒经辰所入馀，为转馀。应增者，减法。应减者，因馀。皆以乘率差，总法而一，加于通率。变率乘之，总法而一，以速减迟加变率为定率。乃以定率增减迟速积为定。此法微密至当，以示算理通途。若非朔望有及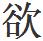考校速要者，但以入馀乘增减率，总法而一，增减速为要耳。其后无同率者，亦因前率，应增者以通率为初数，半率差而减之；应减入馀进退者分为二，随馀初末，如法求之。所得并以加减变率为定。

其入前件馀，如初数已下者为初，已上者以初数减总法，馀为末之数。增减相反，约以九分为限。初虽少弱，而末微强，馀差不多，理况兼举，皆今有杂差，各随其数。若恆算所求，七与二十一得初率，而末之所减，隐而不显。且数与平行正算，亦初末有数，而恆算所无。其十四、二十八既初末数存，而虚差亦减其数，数当去恆法不见。

求朔弦望盈朒所入名及小馀术各以其所入变历速定数速减迟加其盈朒小馀。若不足，进退其。命以甲子算外，各其盈朒反馀。加其恆，馀者为盈；减其恆，馀者为朒。其不动者，依恆朔而定其小馀，推拟月行度。其定小馀二十四已下，一千三百一十六已上者，其入气盈朒、入历迟速，皆须覆依本术推算，不得从举速要之限。乃前朔后朔，迭相推校。盈朒之课，据实为准。损不侵朒，益不过盈。

求定朔月大小术凡朔盈朒名，即为定朔名。其定朔名，十干与来月同者大，不同者小。其月无中气者为闰月。其正月朔有定加时正月者，消息前后各一两月，以定月之大小。合亏在晦二者，弦望亦随事消息。凡置月朔，盈朒之极，不过频三。其或过者，观定小馀近夜半者量之。

检宿度术前件周天二十八宿，相距三百六十五度，前汉唐都以浑仪赤道所量。其数常定，纮带天中，仪图所准。月往来，随损益。所入宿度，进退不同。

黄道宿度左中郎将贾达检月所去赤道不同，更铸黄道浑仪所检者。

臣等今所修撰讨论，更造木浑图络调赋黄赤二道三百六十五度有奇，校量大率，与此符会。今历以步行月及五星出入循此。其月行络黄道，进退亦宜有别。每辄差，不可详尽。今亦依黄道推步。

推躔术置冬至初躔差率，加总法，乘冬至小馀，如总法而一，以减天宿度分。其馀命起黄道斗十二度，宿次去之，经斗去宿分度，不宿算外，即所求年冬至夜半所在宿度算及分。

求每定气初夜半所在定度术各以其定气初躔差率，乘气定馀，总法而一，进加退减馀为分，以减定气度及分，命以宿次如前，即其夜半度及秋二分定气初为进退之始，当平行一度。自馀依进加退减度之。

求次夜半所在定度术各因定气夜半所在为本，加度一。又以其躔差率，进加退减度分。若不足，并依前例。去命如上，即得所求。其定朔弦望夜半度，各随定气，以其月名亦直而分别之。勘右依恆有馀，从定恆行度，不用躔差。

求朔弦望定夜辰所加度术各以其定小馀为平分。又定小馀乘其所躔差率，总法而一，乃进加退减其平分，以加其夜半度，即各定辰所加。其与五星加减者，半其分，消息月朔者，应推月度所须，皆依本朔大小。若注历，依甲子乙丑各拟入。

推月离术求朔望定辰月所在度术各置朔弦望定辰所加度及分。

凡朔定辰所加为合朔，月同度。上弦加度九十一、分四百一十七。

望加度一百八十三、分八百三十四。

下弦加度二百七十三、分一千二百五十一。讫，各半而十退之，为程度分。

求次月定朔夜半入变历术置天正恆朔夜半所入变及馀。定朔有进退一者，进退一，为定朔夜半所入。

月大加二，月小加一。馀皆五百九十六、奇十六。

求次夜半所入变历术因定朔夜半所入算，加一，皆如前。其弦皆依前定所在求之。

求变定离程术各以其夜半入变馀，乘离差，总法而一，为见差。以进加退减其离程，为月每所离定程。

求朔弦望之定夜半月所在度术各以其定小馀，乘所入变离定程，总法而一，为夜半后分。程法为度，馀为度分。以减其加辰所在度及分，命以黄道宿度，即其所求。次夜半，各以离定程加朔弦望夜半所在分，程法从度，去命以黄道宿度算外，则次夜半月度。求晨昏度，以其离定程乘其夜刻，二百而一，为昏分，程法为度。望前以昏，后以晨，加夜半度，得所求。其弦望以五乘定小馀，程法一，为刻，即各其辰所入刻数。皆减其晨前刻，不尽为晨后刻。不晨前刻者，从前注历，伺候推。

总刻:一百。辰刻:分十一。刻分法:七十二。

求定气昼夜漏刻及出没术倍其气晨前刻及分，法从刻，为不见漏。以减百刻，馀为见漏。五刻昼漏刻。以昼漏刻减百刻，馀夜漏刻。以四刻十二分加晨前漏刻，命起子初刻算外，即出辰刻。以见漏加出刻辰，以次如前，即没所在辰刻。以二十五除从夜漏，得每更一筹之数。以二刻三十六分加没辰刻，即甲辰刻，又以更筹数加之，得甲夜一筹数。以次累加，辰去命之，即五更夜筹所以当辰刻及也，以配二十一箭漏之法也。

求每并屈申数术每气准为一十五，各置其气屈申率。每以发敛差损益之，差十从分，分十从率一，即各每屈申率。各累计屈申率为刻分，乃以一百八十乘刻分，泛差十一乘纲纪而除之，得为刻差，法为刻。随气所在，以申减屈加不见漏而半之，为晨前定刻。每求次，各如前法。时加其如始，随加辰晚，以率课之。

求黄道去极每差术置刻差，三十而一为度。不三约为分。申减屈加其气初黄道度，即每所求。

求昏旦去中星度术每求其昼漏刻数，以乘期实，二百乘总法而除之，得昏去中星度。以减周天度，馀为晨去中星度。以昏旦去中星度，加其辰所在，即各其中宿度。其梗概举者，加其夜半度，各其中星宿度。

因求次者，各置其四刻差，七十二乘之，二百八十八而一度。冬至后加，夏至后减。随加，各得每去中度。晨昏所距在黄道中星准度，以赤道计之。其赤道同太初星距。

推游术终率:一千九十三万九千三百一十三。奇率:三百。

约终:三万六千四百六十四奇一百一十三。